S15-07 算法-堆结构
[TOC]
堆结构
概述
堆
堆(Heap) 是一种特殊的树形数据结构,堆的特点是每个节点的值都与其子节点的值进行比较,满足特定的堆性质。通常用于实现优先队列、动态排序等应用。
堆相对于前面的数据结构来说,要稍微难理解一点。
实现:堆使用完全二叉树来实现
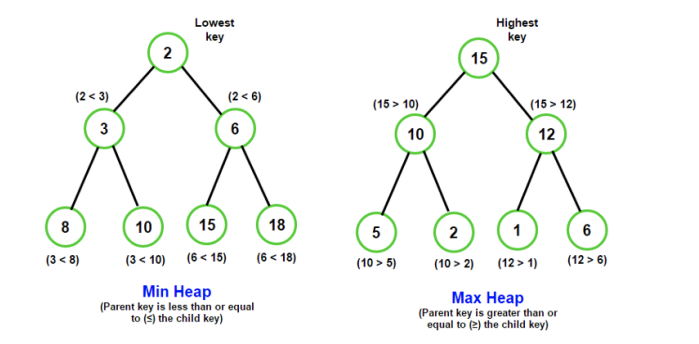
分类:堆可以进行很多分类,但是平时使用的基本都是二叉堆;二叉堆又可以划分为最大堆和最小堆;
- 最大堆(Max Heap):每个父节点的值
>=其子节点的值。 - 最小堆(Min Heap):每个父节点的值
<=其子节点的值。
最值问题
对于每一个新的数据结构,我们都需要搞清楚为什么需要它,这是我们能够记住并且把握它的关键。它到底帮助我们解决了什么问题?
案例:获取集合的最大、最小值:
如果有一个集合,我们希望获取其中的最大值或者最小值,有哪些方案呢?
- 数组/链表:时间复杂度是O(n)。
- 优化方法:可以进行排序,但是我们只是获取最大值或者最小值而已,但排序本身就会消耗性能;
- 哈希表:不需要考虑了;
- 二叉搜索树:时间复杂度是O(logn)。
- 缺点:二叉搜索树操作较为复杂,并且还要维护树的平衡时才是O(logn)级别;
- 堆结构:推荐,这个时候需要一种数据结构来解决这个问题,就是堆结构。
堆的特性
用途 :堆结构通常是用来解决Top K问题的
- Top K问题 是指在一组数据中,找出最前面的K个最大/最小的元素;常用的解决方案有使用排序算法、快速选择算法、堆结构等;
表现形式:二叉堆用树形结构表示出来是一颗完全二叉树。
底层实现:底层会使用数组来实现。
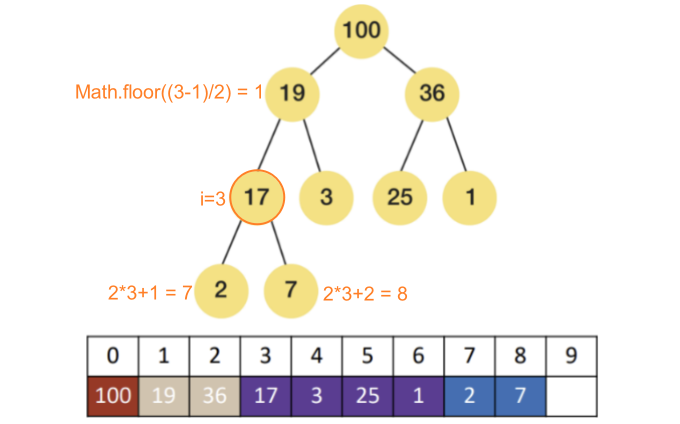
索引计算公式:每个节点在数组中对应的索引i有如下的规律:
- 如果
i = 0,它是根节点 - 父节点:
Math.floor((i–1)/2) - 左子节点:
2i+1 - 右子节点:
2i+2
最大堆的实现
API
接下来,让我们对堆结构进行设计,看看需要有哪些属性和方法。
常见属性:
- data:
,存储堆中的元素,通常使用数组来实现。 - size:
,堆中当前元素的数量。
常见方法:
- insert():
(value),在堆中插入一个新元素。 - extract() / delete():
(),从堆中提取/删除最大或最小元素。 - peek():
(),返回堆中的最大或最小元素。 - isEmpty():
(),判断堆是否为空。 - build_heap():
(list),通过一个列表来构造堆。
那么接下来我们就来实现这个堆结构吧!
封装-Heap
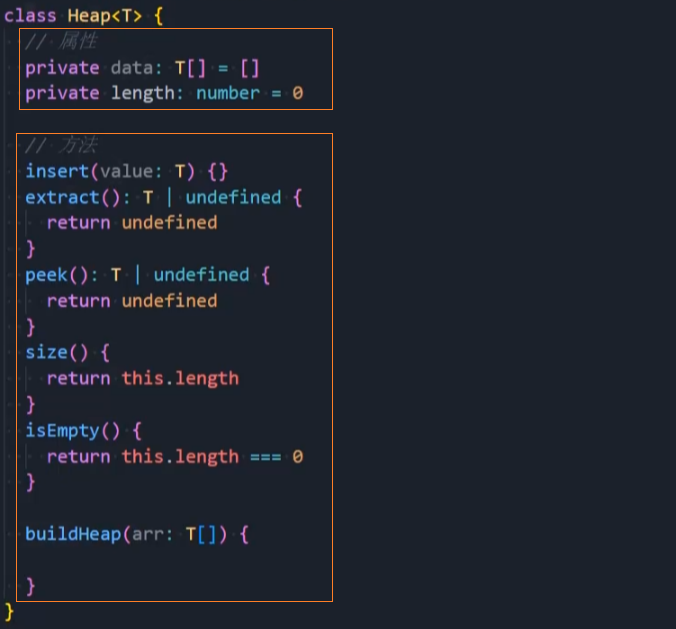
封装Heap的类:
- data:
,存储堆中的元素,通常使用数组来实现。 - size:
,堆中当前元素的数量。
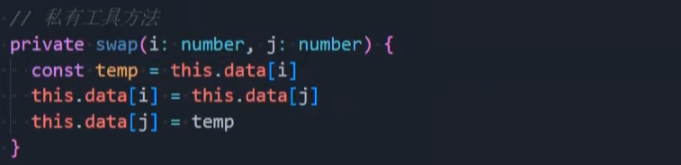
封装-swap()
swap():(i,j),私有方法,交换i和j这2个值。
封装-peek()
peek():(),返回堆中的最大或最小元素。

封装-size()
size():(),堆中当前元素的数量。

封装-isEmpty()
isEmpty():(),判断堆是否为空。

封装-insert()
insert():(value),在堆中插入一个新元素。
最大堆插入思路:每次插入元素后,需要对堆进行重构,以维护最大堆的性质,该维护策略称为上滤(percolate up)。
1、将新元素直接添加到数组的最后位置
2、检测是否符合最大堆的特性:
- 符合:不再操作
- 不符合:将新插入的元素进行上滤操作:
上滤操作:
- 1、新元素索引:
index = data.length - 1 - 2、父元素索引:
parentIndex = Math.floor((index - 1) /2) - 3、将新元素和父元素进行比较:
- 如果新元素
<=父元素,直接break - 如果新元素
>父元素,交换二者swap,同时修改index为父元素的索引parentIndex
- 如果新元素
- 4、进行下一次循环操作,直到
index <= 0
- 1、新元素索引:
图解:
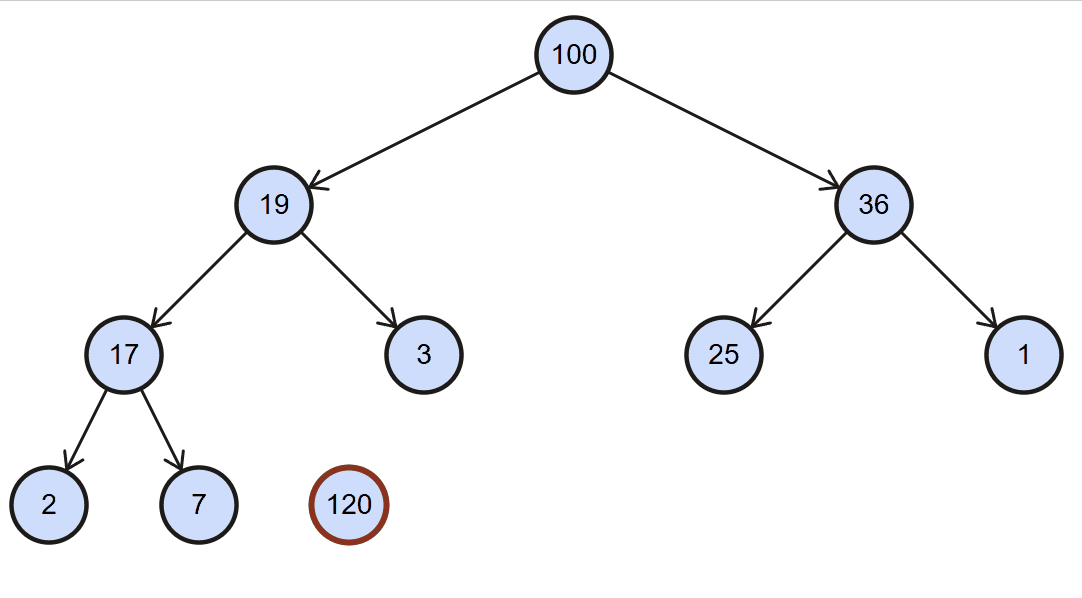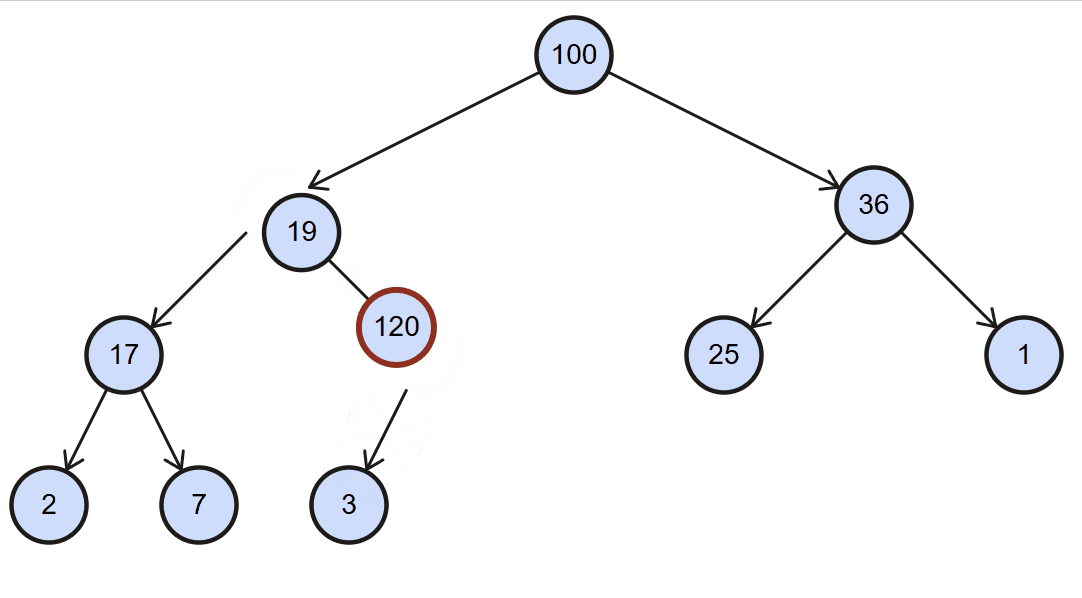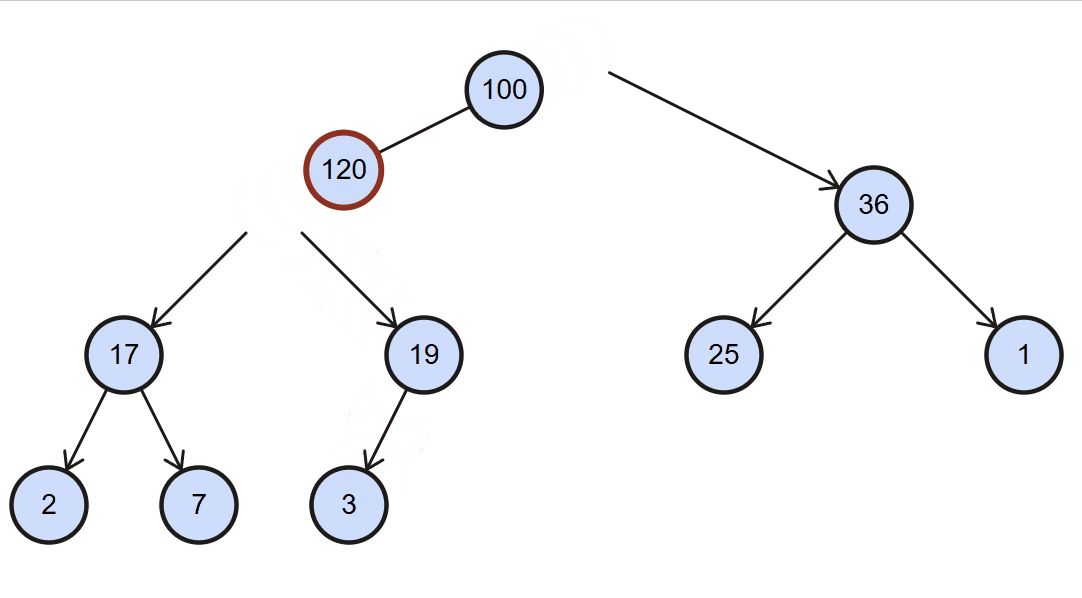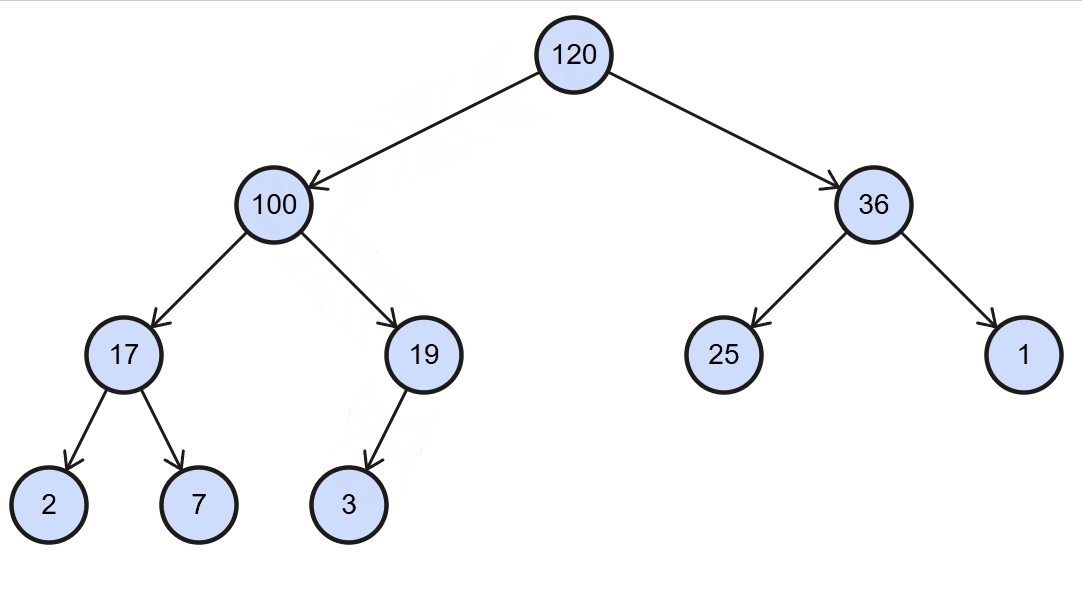
代码实现:
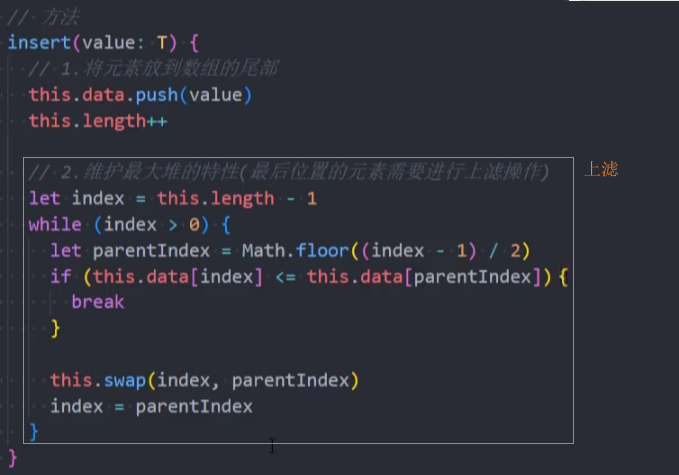
测试: [19, 100, 36, 17, 3, 25, 1, 2, 7]
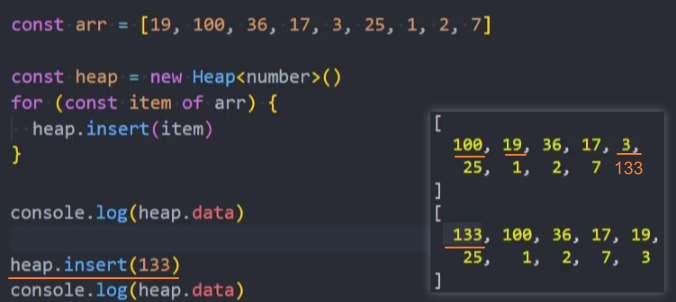
代码抽取:
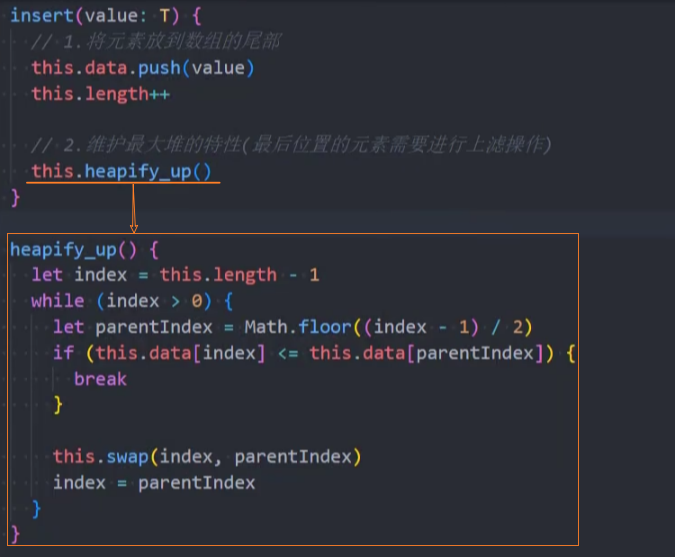
封装-delete()@
extract() / delete():(),从堆中提取/删除最大或最小元素。
最大堆删除思路:每次删除元素后,需要对堆进行重构,以维护最大堆的性质,该维护策略称为下滤(percolate down)。
- 1、将最后的元素赋值给被删除元素,这样不会破坏最大堆的结构
- 2、对最后的元素进行下滤操作:
- 下滤操作:
- 1、当前节点(最后的节点)索引:
index=0 - 2、左子节点索引:
leftChildIndex = 2 * index + 1 - 3、右子节点索引:
rightChildIndex = 2 * index + 2 - 4、比较2个子节点值的大小,找到较大的值:
largerIndex - 5、比较当前节点和较大的子节点的值:
- 如果子节点值
=<当前节点,直接break - 如果子节点值
>当前节点,交换二者swap,同时修改index为largerIndex
- 如果子节点值
- 6、进行下一次循环操作,直到
2*index + 1 >= this.length
- 1、当前节点(最后的节点)索引:
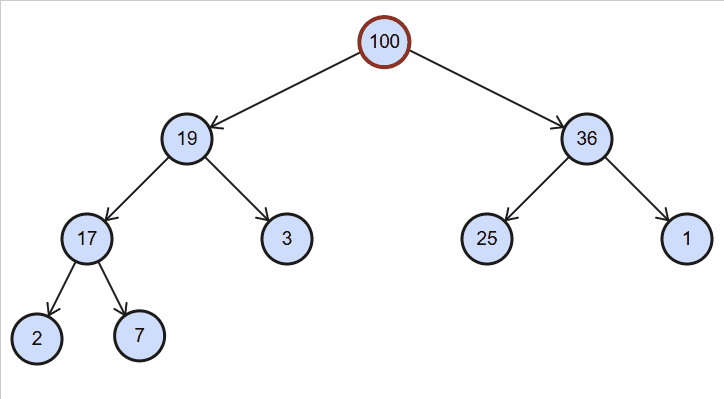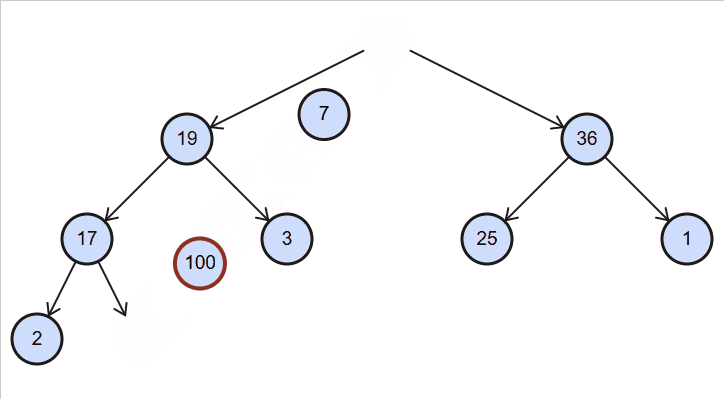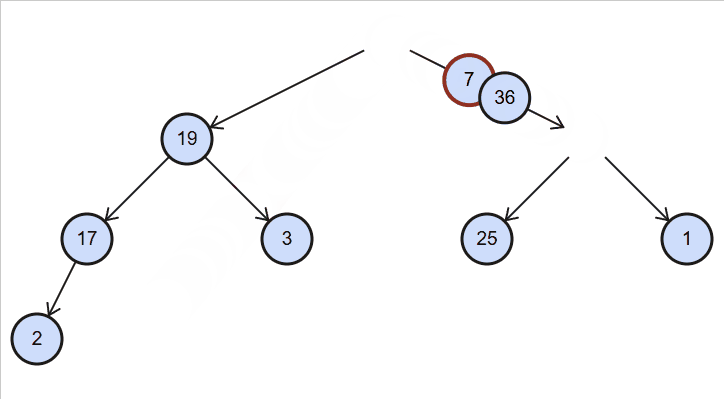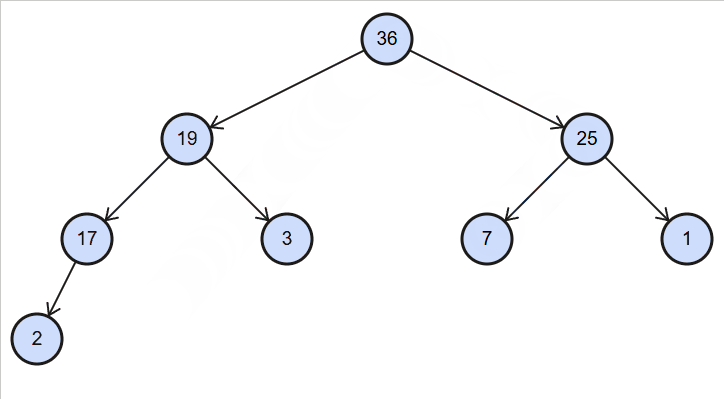
图解:
删除120

删除100
代码实现:
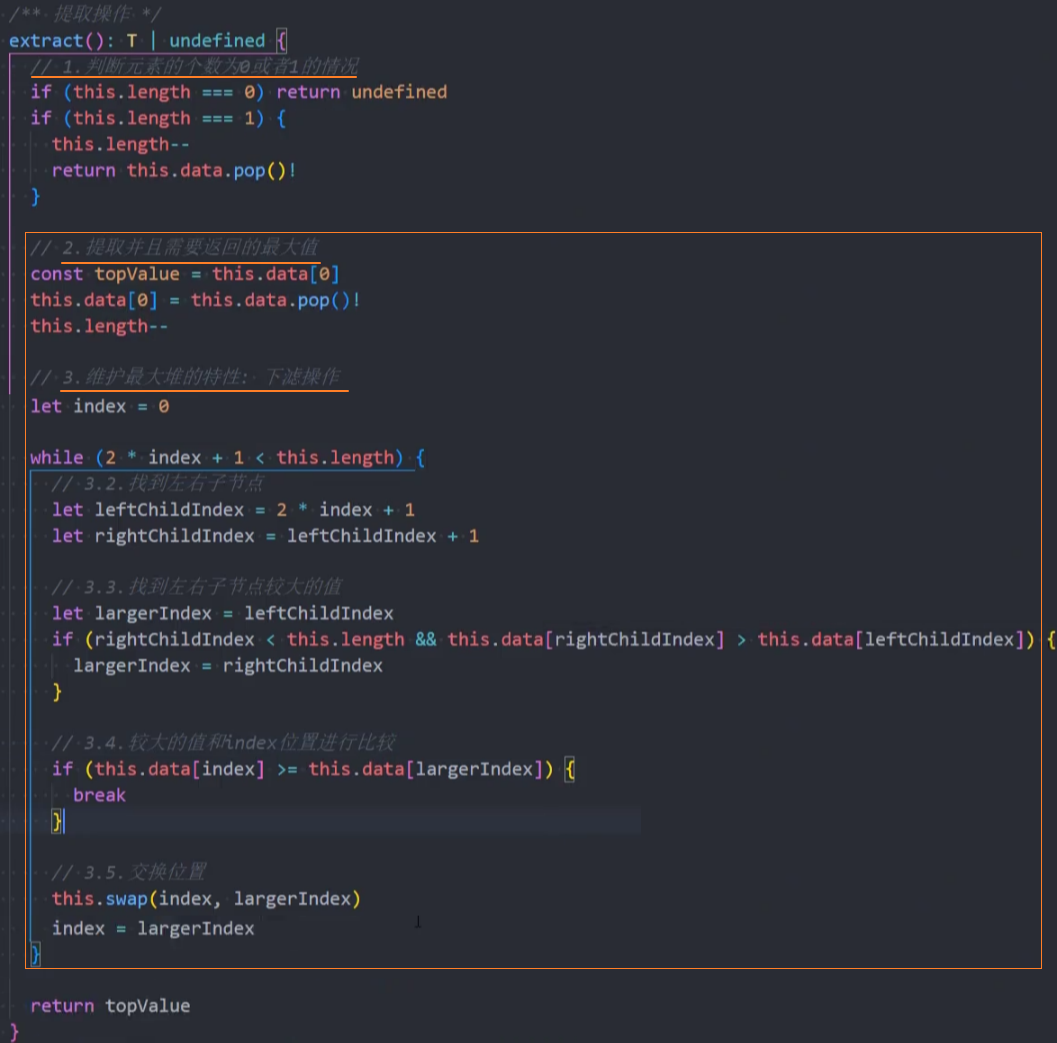
测试: 从大到小依次弹出

封装-buildHeap()@
build_heap():(list),通过一个列表来构造堆。
原地建堆(In-place heap construction) 是指建立堆的过程中,不使用额外的内存空间,直接在原有数组上进行操作。
实现思路:从最后一个非叶子节点开始依次执行下滤操作,直到堆顶。
图解: [9,11,20,56,23,45]

代码实现:
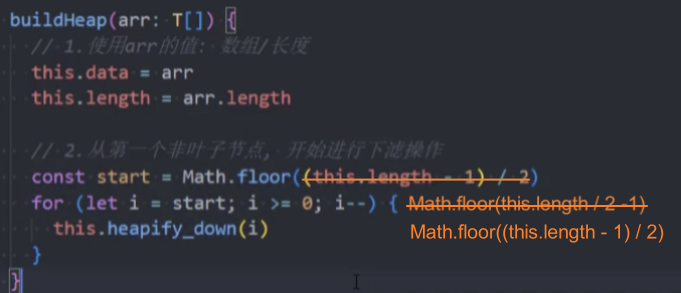
测试:
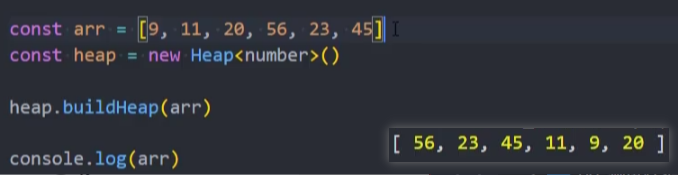
这种原地建堆的方式,我们称之为自下而上的下滤。也可以使用自上而下的上滤,但是效率较低,作为课下自行研究。
优化:在构造函数中原地建堆
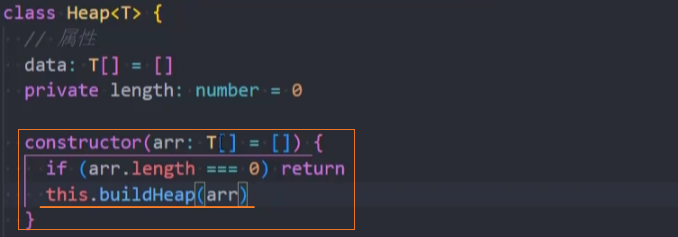
最小堆的实现
1、修改插入操作的heapify_up()方法
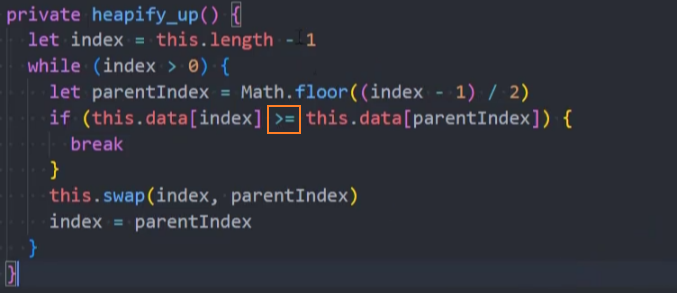
测试:
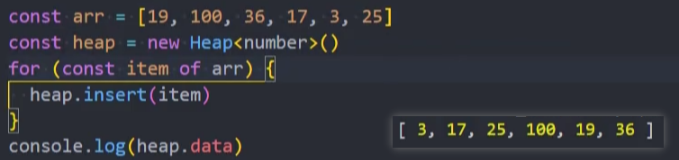
2、修改删除操作的heapify_down()方法
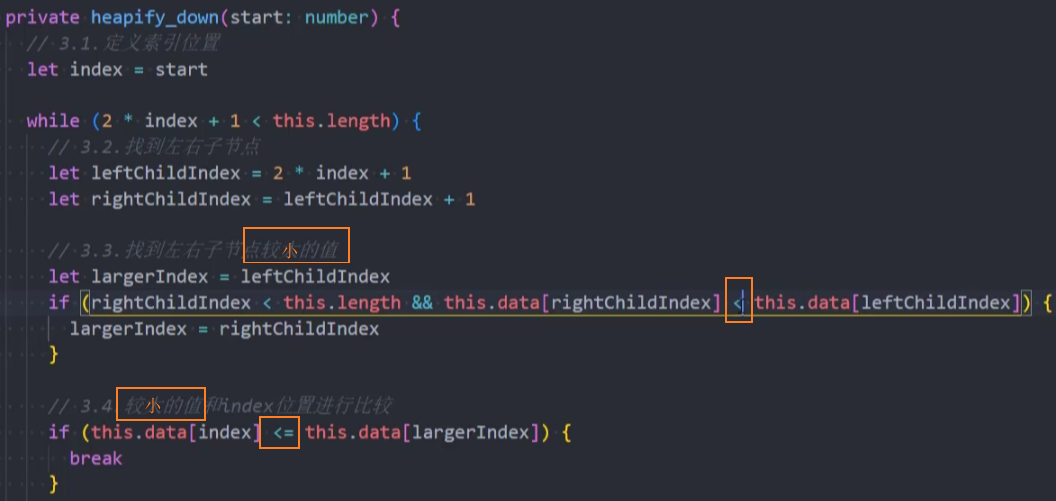
测试:

二叉堆的实现
在一个类中同时实现最大堆和最小堆,根据传入的参数isMax不同分别生成最大堆和最小堆。
1、添加isMax属性,标记最大堆、最小堆
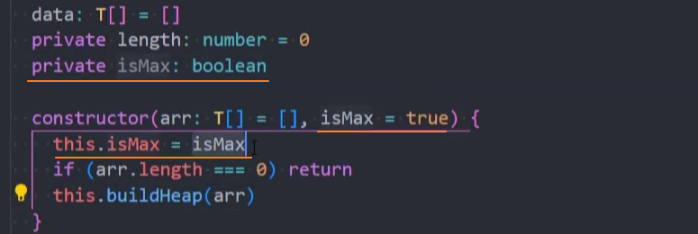
2、封装私有方法,比较2个索引的值
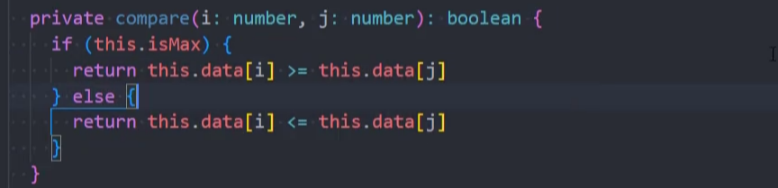
3、修改heapify_up()方法,调用compare()方法进行比较
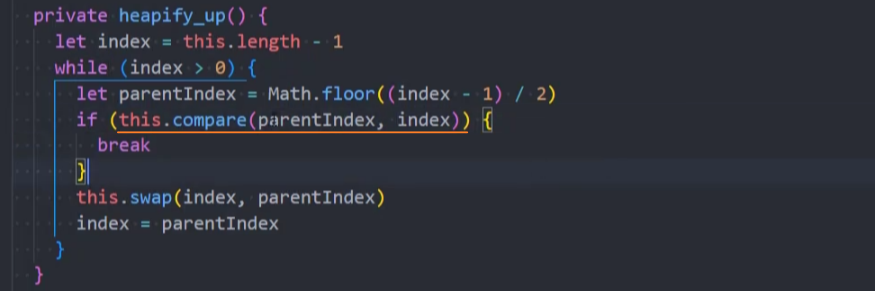
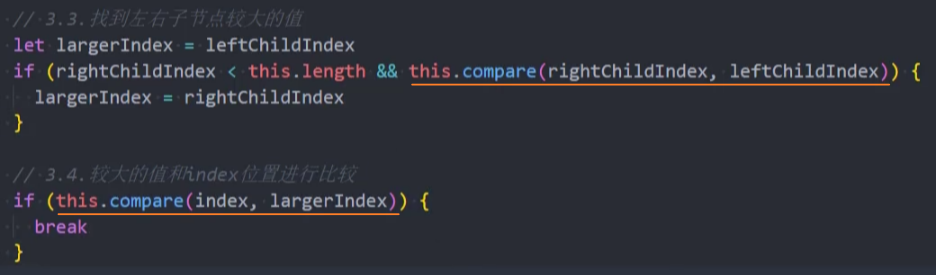
4、修改heapify_down()方法,调用compare()方法进行比较
数据结构可视化网站
在线数据结构演练: